Hay una pregunta que nadie formula. ¿Si la tasa de mortalidad y distribución por edades es la misma en todos los continentes, porque varían la curva de contagios y el número de muertos en los distintos países? ¿Si la tasa de contagio es la misma, cómo es posible que la forma de la curva sea diferente de una región a otra?

Tres ejemplos, para ilustrarlo:

1.Brasil, México, India. Parábola.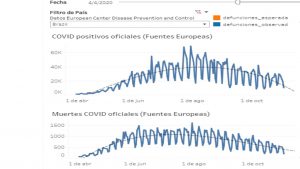

2. Marruecos. Función lineal

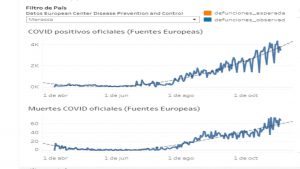
3. Francia, Italia, Reino Unido. Función exponencial

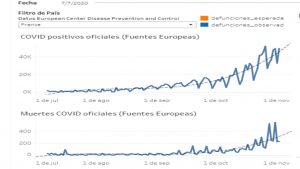Los estudios de la mortalidad y distribución por edades en todos los continentes dejan gráficos como estos:

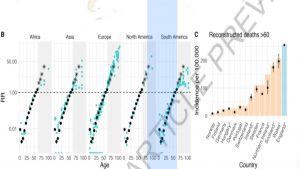La respuesta lógica tiene que ver con la Inmunidad de Rebaño y el tipo de muertes que se analizan. Si todo el mundo entiende que no es lo mismo una defunción por accidente de tráfico que por enfermedad, tampoco lo es sufrir un infarto o padecer una neumonía.

Si bien el incremento de la mortalidad (exceso) guarda una correlación evidente con la esperanza de vida, no es suficiente para explicar porque en Japón no han muerto tantos ancianos como en España o Italia. Encontramos una pista si comparamos la estadística global del otoño en cada región. En España, sin ir más lejos, el incremento es notable pero se mantiene constante en torno al 25%.

1. Octubre de 2018 (30.383)
2. Octubre de 2019 (30.266)
3. Octubre de 2020 (37.100)
Fuente: Servicio Vigilancia de la Mortalidad Diaria y Carlos Iglesias

Tasa de contagio en el mundo

Si la tasa de contagio y la de letalidad se mantienen invariables en todo el mundo en torno al 2/1000: ¿Cómo es posible que la tasa de contagio esté superando el 5% en muchos países de Europa? ¿A qué se debe este nuevo brote?
A bote pronto, la intuición nos estaría indicando que ha cambiado la metodología y el criterio de los tests. ¿Es, tal vez, una manera curarse en salud? Disparar la alarma social para poder justificar las medidas de confinamiento de cara a la Navidad? Da la sensación de que se equivocan. Su estrategia parte de premisas erróneas.

(c) Belge